Question

To factor the quadratic expression x^2−8x−10 by completing the square, what value would be added? A. 64 B. 8 C. 16 D.-16

Answer 1

A quadratic function equation is as follows:

`ax^(2) + bx + c`

To complete the square, move the constant (c) to the other side of the equation and take half of the b value, square it, and add and subtract the same number.

In this problem, you will add 16.

`( - 8)/(2) = - 4`

`- 4^(2) = 16`

Answer 2

C

Explanation:

When completing the square, we essentially want to create a perfect square trinomial by adding a constant.

If we have the following expression:

`x^2+bx`

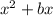
And we want to complete the square, we will need to divide the b-coefficient by half and then square it.

Thus, the added term should be:

`(b/2)^2`

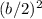
In the given equation, we have:

`(x^2-8x)-10`

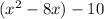
The b term here is 8. Therefore:

`(8/2)^2\\=(4)^2\\=16`

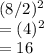
The value we would add would be 16.

The answer is C.

Further notes:

To complete the square, add 16 like mentioned earlier. However, we also need to subtract 16 to balance things out:

`(x^2-8x)-10\\=(x^2-8x+16)-10-16\\`

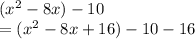
The expression inside the parentheses is now a perfect square trinomial. Factor it:

`=((x)^2-2(4)(x)+(4)^2)-26\\=(x-4)^2-26`

And we are done!