Question

What are the explicit equation and domain for a geometric sequence with a first term of 5 and a second term of −10? an = 5(−2)n − 1; all integers where n ≥ 1 an = 5(−2)n − 1; all integers where n ≥ 0 an = 5(−15)n − 1; all integers where n ≥ 1 an = 5(−15)n − 1; all integers where n ≥ 0

Answer 1

A

Explanation:

The standard form of an explicit formula for a geometric sequence is given by:

`x_n=a(r)^(n-1)`

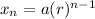
Where n is the nth term, a is the initial term, and r is the common ratio.

We are given that the first term is 5. Hence, a = 5.

Also, we are given that the second term is -10. Therefore, the common ratio r is -2, because we multiply the first term by -2 to acquire -10.

Substituting yields:

`x_n=5(-2)^(n-1), n\geq 1, n\in\mathbb{Z}`

(Note: Z means the set of all integers. This is required because the term number can only be positive starting from one. For instance, we can't have the 0th term or the 1.5th term.)

In conclusion, the answer is A.