Explanation:
A playing card is in the form of a rectangle whose perimeter is equal to 28 cm and area is 45 cm².
If l and b are length and breadth of the rectangle.
Area,
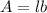
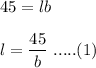
Perimeter,
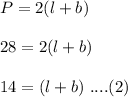
Put the value of l from equation (1) to equation (2). So,
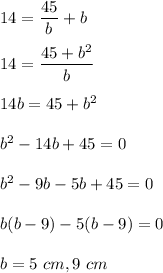
Put the value of b in equation (1),
If b = 5 cm
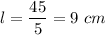
If b = 9 cm
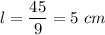
So, the dimensions of the playing card is 9 cm by 5 cm.