Question

A wheel rotating about a fixed axis has a constant angular acceleration of 4.0 rad/s2. In a 4.0-s interval the wheel turns through an angle of 80 radians. Assuming the wheel started from rest, how long had it been in motion at the start of the 4.0-s interval?

a. 3 s.
b. 6 s.
c. 9 s.
d. 12 s.

Answer 1

a. 3 s.

Step-by-step explanation:

Given;

angular acceleration of the wheel, α = 4 rad/s²

time of wheel rotation, t = 4 s

angle of rotation, θ = 80 radians

Apply the kinematic equation below,

`\theta = \omega_1 t \ + \ (1)/(2) \alpha t^2\\\\80 = 4\omega_1 + (1)/(2)*4*4^2\\\\80 = 4\omega_1 + 32\\\\ 4\omega_1 = 48\\\\ \omega_1 = (48)/(4)\\\\ \omega_1 = 12 \ rad/s`

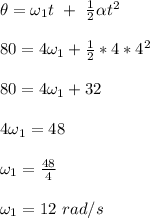
Given initial angular velocity, ω₀ = 0

Apply the kinematic equation below;

`\omega_1 = \omega_o + \alpha t_1\\\\12 = 0 + 4t\\\\4t = 12\\\\t = (12)/(4)\\\\t = 3 \ s`

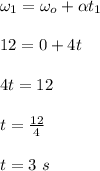
Therefore, the wheel had been in motion for 3 seconds.

a. 3 s.