Answer:
Given series is divergent
Explanation:
Step(i):-
By using Ratio test
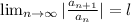
a)
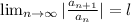
'l' is finite then the given ∑aₙ is convergent
b)
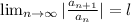
Here 'l' is infinite then the ∑aₙ is divergent
Step(ii):-
Given aₙ =
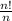
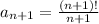
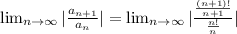
we know that n ! = n (n-1) (n-2) ......3.2.1
and also (n+1) ! = (n+1)n!
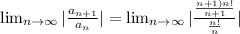

= ∞
Given sum of the series is divergent