Question

Suppose the roots of the polynomial $x^2 - mx + n$ are positive prime integers (not necessarily distinct). Given that $m < 20,$ how many possible values of $n$ are there?

Answer 1

18 values for n are possible.

Explanation:

Given the quadratic polynomial:

`$x^2 - mx + n$`

such that:

Roots are positive prime integers and

`$m < 20$`

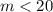
To find:

How many possible values of
`n` are there ?

Solution:

First of all, let us have a look at the sum and product of a quadratic equation.

If the quadratic equation is:

`Ax^(2) +Bx+C`

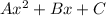
and the roots are:
`\alpha` and
`\beta`

Then sum of roots,
`\alpha+\beta = -(B)/(A)`

Product of roots,
`\alpha \beta = (C)/(A)`

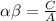
Comparing the given equation with standard equation, we get:

A = 1, B = -m and C = n

Sum of roots,
`\alpha+\beta = -(-m)/(1) = m`

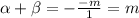
Product of roots,
`\alpha \beta = (n)/(1) = n`

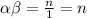
We are given that
`m<20`

`\alpha` and
`\beta` are positive prime integers such that their sum is less than 20.

Let us have a look at some of the positive prime integers:

2, 3, 5, 7, 11, 13, 17, 23, 29, .....

Now, we have to choose two such prime integers from above list such that their sum is less than 20 and the roots can be repetitive as well.

So, possible combinations and possible value of
`n (= \alpha * \beta)` are:

`1.\ 2, 2\Rightarrow n = 2* 2 = 4\\2.\ 2, 3 \Rightarrow n = 6\\3.\ 2, 5 \Rightarrow n = 10\\4.\ 2, 7\Rightarrow n = 14\\5.\ 2, 11 \Rightarrow n = 22\\6.\ 2, 13 \Rightarrow n = 26\\7.\ 2, 17 \Rightarrow n = 34\\8.\ 3, 3\Rightarrow n = 3* 3 = 9\\9.\ 3, 5 \Rightarrow n = 15\\10.\ 3, 7 \Rightarrow n = 21\\`

`11.\ 3, 11\Rightarrow n = 33\\12.\ 3, 13 \Rightarrow n = 39\\13.\ 5, 5 \Rightarrow n = 25\\14.\ 5, 7 \Rightarrow n = 35\\15.\ 5, 11 \Rightarrow n = 55\\16.\ 5, 13 \Rightarrow n = 65\\17.\ 7, 7 \Rightarrow n = 49\\18.\ 7, 11 \Rightarrow n = 77`

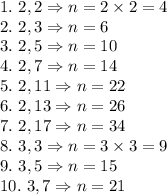
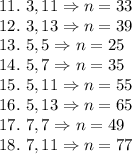
So,as shown above 18 values for n are possible.