Question

Which of the following is NOT a formula for determining complementary probability?

Answer 1

Question:

Which of the following is NOT a formula for determining complementary probability?

A. P(outcome) = 1- P(-outcome)

B. P(outcome) - P(-outcome) = 1

C. P(outcome) + P(-outcome) =1

D. P(-outcome) = 1 - P(outcome)​

Answer:

`P(outcome) - P(-outcome) = 1`

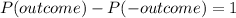
Explanation:

Required

Determine which option is not a formula of complementary probabilities

From the list of given options, the complementary probabilities are P(outcome) and P(-outcome)

In probability;

`P(outcome) + P(-outcome) = 1` --- Equation 1

Subtract P(outcome) from both sides

`P(outcome) - P(outcome) + P(outcome) = 1 - P(outcome)`

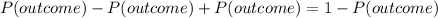
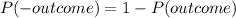`P(-outcome) = 1 - P(outcome)` ------ Equation 2

Subtract P(-outcome) from both sides of equation 1

`P(outcome) + P(-outcome) - P(-outcome) = 1 - P(-outcome)`

`P(outcome) = 1 - P(-outcome)`

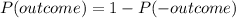
Equation 1, 2 and 3 represents options A, C and D

While option B is out of place

Hence, option B is not a formula of complementary probability