Answer:
a = -1 and
b = 10
Explanation:
Given:
h(x) = (x – 1)³ + 10
h(x) = (g compose f)(x).
f(x) = x + a and
g(x) = x³ + b
To find:
The values of a and b = ?
Solution:
First of all, let us have a look at the composite functions.
(g compose f)(x) means we replace the value of
 with
with
 in the function
in the function
 .
.
We know that:
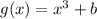 and
and

Let us find (g compose f)(x) by replacing
 with
with

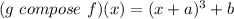
Also, h(x) = (g compose f)(x) = (x – 1)³ + 10
Therefore,
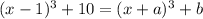
Comparing the corresponding elements of the above expressions:
we get a = -1 and
b = 10