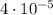Answer:
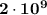
Explanation:
The given expression s are:
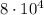 and
and
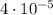
To find:
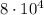 is how many times as large as
is how many times as large as
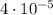 .
.
Solution:
Let
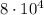 is
is
 times as large as
times as large as
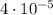 .
.
So, we can say that:
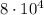 =
=
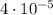


OR
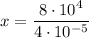
Let us have a look at the formula for exponents:
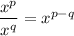
Here we have:
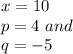
Solving the expression using above formula:
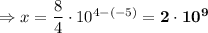
So, Let
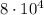 is
is
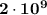 times as large as
times as large as