Question

Flying against the wind, a jet travels 2920 miles in 4 hours. Flying with the wind, the same jet travels 7140 miles in 6 hours. What is the rate of the jet in still air and what is the rate of the wind

Answer 1

Rate of jet in still air = 960 miles/ hr

Rate of the wind = 230 miles/ hr

Explanation:

Let the speed of jet in still air =
`u` miles/hr

Let the speed of air =
`v` miles/hr

So, against the wind, the resultant speed =
`(u-v)` miles/hr

And, with the wind, the resultant speed =
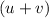`(u+v)` miles/hr

Distance traveled against the wind = 2920 miles

Time taken against the wind = 4 hrs

Formula for distance is:

`\bold{Distance =Speed * Time}`

`2920 = (u-v)* 4\\\Rightarrow u-v=(2920)/(4)\\\Rightarrow u-v=730\ miles/hr...... (1)`

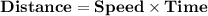
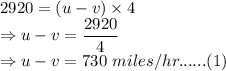
Distance traveled with the wind = 7140 miles

Time taken against the wind = 6 hrs

`\bold{Distance =Speed * Time}`

`7140 = (u+v)* 6\\\Rightarrow u+v=(7140)/(6)\\\Rightarrow u+v= 1190 \ miles/hr...... (2)`

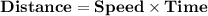
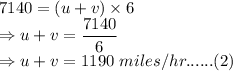
Adding (1) and (2):

`2u = 1920\\\Rightarrow \bold{u = 960 miles/hr}`

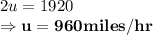
Putting
`u` in (1):

`960 -v = 730 \\\Rightarrow \bold{v=230\ miles/hr}`

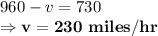
Therefore, the answer is:

Rate of jet in still air = 960 miles/ hr

Rate of the wind = 230 miles/ hr

Answer 2

Velocity in still air is = 960 miles per hour

Velocity of wind = 230 miles per hour.

Explanation:

The velocity when flying against the wind = 2920 / 4 = 730 miles per hour.

The velocity when flying with the wind = 7140 / 6 = 1190

Let the rate of jet in still Air = x

Let the rate of jet in wind = y

Therefore, velocity against wind = x-y and wind = x + y

x - y = 730

x + y = 1190

Add both equation, 2x = 1920

x = 960

Now find the value of “y” = 1190 – 960 = 230

Thus, velocity in still air is = 960 miles per hour

Velocity of wind = 230 miles per hour.