Answer:
a. P(X<68) = 0.9082
b. P(61 < X< 70) = 0.8185
c. the gestation period that corresponds to the top 10% of gestation periods = 67.846
d. the gestation period that corresponds to the 25th percentile = 61.977
Step-by-step explanation:
Given that:
population mean
 = 64
= 64
standard deviation
 = 3
= 3
a. What proportion of kittens have a gestation period of less than 68 days?
here the sample mean x = 68
The standard normal distribution for the z score is
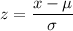
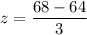
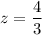
z = 1.33
The proportion of the kittens having a gestation period of less than 68 days is:
P(X<68) = P(Z< 1.33)
Using the z - tables
P(X<68) = 0.9082
b. What proportion of kittens have a gestation period between 61 and 70 days?
here ; sample mean x₁ = 61 and x₂ = 70
the standard normal distribution for the z score is:
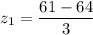
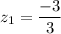
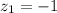
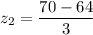
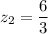
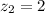
So, the proportion of kittens having a gestation period between 61 and 70 days is:
P(61 < X< 70) = P(-1 < Z < 2)
P(61 < X< 70) = P(Z < 2) - P( Z< -1)
From z tables
P(61 < X< 70) = 0.9772 - 0.1587
P(61 < X< 70) = 0.8185
c. What gestation period corresponds to the top 10% of gestation periods?
i.e
P(X >
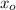 ) = 0.1
) = 0.1
P(X <
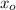 ) = 1 - 0.1
) = 1 - 0.1
P(X >
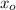 ) = 0.9
) = 0.9
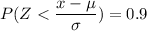
Using the Excel Function : =NORMINV (0.9)

⇒



given that:
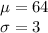
x = 1.282 × 3 + 64
x = 67.846
The gestation period that corresponds to the top 10% of gestation periods = 67.846
d. What gestation period corresponds to the 25th percentile?
At 25 percentile, using the EXCEL FUNCTION = NORMINV(0.25;64;3)
the gestation period that corresponds to the 25th percentile = 61.977