Question

Consider the following data on 20 chemical reactions, with Y = chromatographic retention time (seconds) and X = molecular weight (gm/mole).Retention Time and Molecular Weight Name Retention Time Molecular Weight alpha-pinene 234.50 136.24 Cyclopentene 95.27 68.12 p-diethylbenzene 284.00 134.22 Decane 250.60 142.29 Toluene 174.00 92.14 Benzene 135.70 78.11 2-methylpentane 97.24 86.18 2,3 dimethylbutane 100.70 86.18 1,7-octadiene 172.20 110.20 1,2,4-trimethylbenzene 262.70 120.19 2,3,4-trimethylpentane 160.98 114.23 ethylcyclohexane 195.07 112.22 Limonene 271.50 136.24 methylcyclohexane 153.57 98.19 m-diethylbenzene 281.50 134.22 2,3-dimethylpentane 131.83 100.20 2,2-dimethylbutane 89.34 86.18 Pentane 78.00 72.15 Isooctane 136.90 114.23 Hexane 106.00 86.18 11.value:Required information(a) Write the fitted regression equation. (Negative amount should be indicated by a minus sign.) y = x +ReferenceseBook & ResourcesWorksheetDifficulty: MediumLearning Objective: 12-02Visual Displays and Correlation AnalysisSimple RegressionRegression TerminologyOrdinary Least Squares FormulasTests for SignificanceChapter Exercises12.value:Required information(b) Calculate R2. R2

Answer 1

Answer: (a) y = 2.7394x - 118.1368

(b) R² = 0.8215 or 82.15%

Explanation: Regression line is the best line that relates the variables in the data.

To calculate the fitted regression equation:

1) Calculate average of x-values (
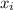`x_(i)`) and average of y-values (
`y_(i)`);

2) Calculate the slope, b, by doing:

`b=(\Sigma (x-x_(i))(y-y_(i)))/(\Sigma (x-x_(i))^(2))`

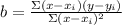
3) Calculate y-intercept, a, by doing:

`a=y_(i)-bx_(i)`

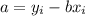
4) Then, it gives regression equation: y = bx + a

For the data on chemical reactions:

(a)
`b=( [(136.24-105.3955)+...+(86.18-105.3955)].[(234.5-170.58)+...+(106-170.58)])/((136.24-105.3955)^(2)+...+(86.18-105.3955)^(2))`

b = 2.7394

`a=170.58-2.7394(105.3955)`

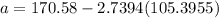
a = -118.1368

y = 2.7394x - 118.1368

The fittest regression equation is y = 2.7394x - 118.1368.

(b) R is correlation coefficient and measures the strength of the relationship between the variables. It is calculated as:

`R=\frac{n\Sigma(xy)-(\Sigma x)(\Sigma y)}{\sqrt{[n\Sigma x^(2)-(\Sigma x^(2))][n\Sigma y^(2)-(\Sigmay^(2))]} }`

For this fit, R = 0.9064

The variable R² is the coefficient of determination, is the square of correlation coefficient and is usually stated as a percent.

What the variable represents is the percent of variation in the dependent variable (y) explained by the variation in the independent variable (x).

For this fit:

`R^(2) = 0.9064^(2)`

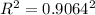
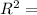`R^(2) =` 0.8215

What it entails is that 82.15% of the variation of retention time is due to the molecular weight of each chemical compound.