Question

The current price of a stock is $55. Calculate the value of an American put option on the stock using a two-step binomial tree given the following information.

The strike price of the option, K = $57, each time step is one year, the risk-free interest rate,
r = 5%, u =1.25, d = 0.8, and p = 0.6282

Answer 1

$5.95

Step-by-step explanation:

Risk neutral probability,
`$ q = ((1+u)^t - d)/(u-d) $`

=
`$ \frac {1.05-0.8}{1.25-0.8} = 0.5556 $`

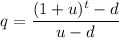
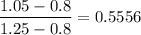
The value of stock lattice is shown below :

85.9375

68.75 55

55 44 35.2

t=0 t=1 t=2

Value of the American put option when the stock price is $85.9375 at t=2

= max(57-85.9375,0) = 0

The value of the American put option when the stock price is $55 at t=2

= max(57-55,0) = 2

The value of American put option when the stock price is $85.9375 at t=2

= max(57-35.2,0) = 21.8

The value of a American put option when the stock price is $68.75 at t=1

= max
`$ (0.5556 * 0 + 0.4444 * 2)/(1.05,57 - 68.75,0) $` = $0.84656

The value of the American put option when stock price is $44 at t=1

= max
`$ (0.5556 * 2 + 0.4444 * 21.8)/(1.05,57 - 44,0) $` = $13

The value of American put option today when the stock price is $55 at t=0

= max
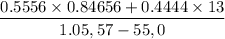`$ (0.5556 * 0.84656 + 0.4444 * 13)/(1.05,57 - 55,0) $` = $ 5.95

Thus, the value of American put option today is $5.95