Answer:
1) The order of the reaction is of FIRST ORDER
2) Rate constant k = 5.667 × 10 ⁻⁴
Step-by-step explanation:
From the given information:
The composition of a liquid-phase reaction 2A - B was monitored spectrophotometrically.
liquid-phase reaction 2A - B signifies that the reaction is of FIRST ORDER where the rate of this reaction is directly proportional to the concentration of A.
The following data was obtained:
t/min 0 10 20 30 40 ∞
conc B/(mol/L) 0 0.089 0.153 0.200 0.230 0.312
For a first order reaction:
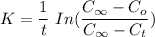
where :
K = proportionality constant or the rate constant for the specific reaction rate
t = time of reaction
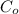 = initial concentration at time t
= initial concentration at time t
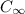 = final concentration at time t
= final concentration at time t
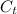 = concentration at time t
= concentration at time t
To start with the value of t when t = 10 mins
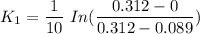

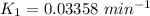
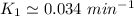
When t = 20
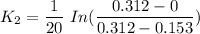
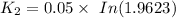
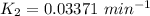
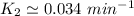
When t = 30
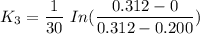
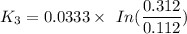
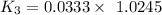
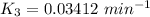
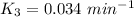
When t = 40
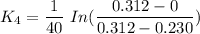
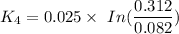
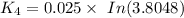

We can see that at the different time rates, the rate constant of
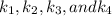 all have similar constant values
all have similar constant values
As such :
Rate constant k = 0.034 min⁻¹
Converting it to seconds ; we have :
60 seconds = 1 min
∴
0.034 min⁻¹ =(0.034/60) seconds
= 5.667 × 10 ⁻⁴ seconds
Rate constant k = 5.667 × 10 ⁻⁴