Answer:
Yes
Step-by-step explanation:
You can find the answer to this question by finding the value of x in both equations.
Let's start off with the first equation:

To find the value of x, you're going to have to subtract 4 from both sides. This is because you're looking for the value of only x, not x + 4. To leave x alone, you'd have to subtract 4, leaving that side with just x.
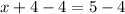

The answer to the first equation is x = 1.
Now let's start on the second equation:
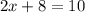
Like before, you're looking for x alone and in this equation, 8 is being added to 2x. Although x itself isn't alone, you'll first start off with 2x since you can simplify it thrughout the process. In this equation, you're going to subtract 8 from both sides to leave the variable x alone.
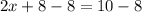
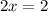
Now you're left with 2x = 2. Since you're looking for the value of x alone, you're going to divide both sides by 2. Because x is being multiplied by 2(2 times x = 2x) you're going to divide(opposite of multiply), which will cancel out the 2(in 2x).
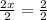

The answer to the second equation is x = 1.
Since both equations have the same solution, the answer to your question would be yes.