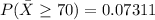Question

Next, the students at the Pearson Cooking Academy are assigned a take-home written exam to assess their knowledge of all things culinary. Historically, students scores on this exam had a N(68, 36) distribution. However, these days, there is an company called Charred Egg that offers to help students on tasks whether or not the exercises are for homework or for exams. In a cohort of 19 students, what is the probability that their average score will be at least 70?

Answer 1

The probability is
`P( \= X \ge 70 ) = 0.07311`

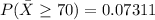
Explanation:

From the question we are told that

The population mean is
`\mu = 68`

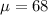
The standard deviation is
`\sigma = √(36) = 6`

The sample size is
`n = 19`

Generally the standard error of the mean is mathematically represented as

`\sigma_(\= x ) = (\sigma )/(√(n) )`

=>
`\sigma_(\= x ) = (6 )/(√(19) )`

=>
`\sigma_(\= x ) = 1.3765`

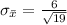
Generally the probability that their average score will be at least 70 is mathematically represented as

`P( \= X \ge 70 ) = 1 - P( \= X < 70 ) = 1 - P(( \= X - \mu )/(\sigma_(\= x)) < (70 - 68)/( 1.3765) )`

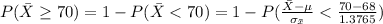
Generally
`( \= X - \mu )/(\sigma_(\= x)) = z(The \ z-score \ of \ \= X )`

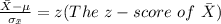
So

`P( \= X \ge 70 ) = 1 - P( \= X < 70 ) = 1 - P(Z <1.453 )`

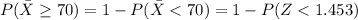
From the z-table

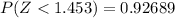
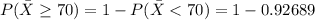
`P(Z <1.453 ) = 0.92689`

=>
`P( \= X \ge 70 ) = 1 - P( \= X < 70 ) = 1 - 0.92689`

=>
`P( \= X \ge 70 ) = 1 - P( \= X < 70 ) = 0.07311`

=>
`P( \= X \ge 70 ) = 0.07311`