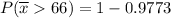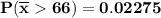Answer:
a.
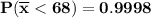
b.
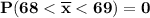
c.
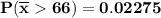
Explanation:
Given that ;
Let Y be a random variable In a population, where:
mean
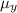 = 65
= 65
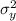 = 49
= 49
standard deviation σ =
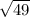 = 7
= 7
The objective is to determine the following :
In a random sample of size n = 69, find Pr(Y <68) =
Using the Central limit theorem
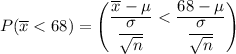
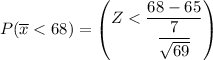
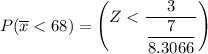
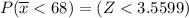
From the z tables:
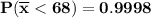
In a random sample of size n = 124, find Pr (68< Y <69)=
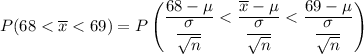
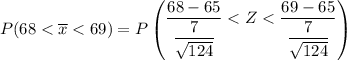
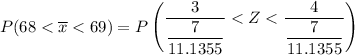
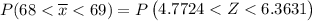
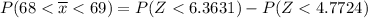
From z tables
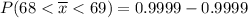
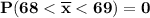
In a random sample of size n = 196, find Pr (Y >66)=
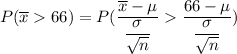
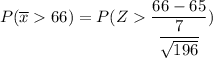
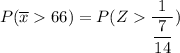
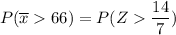
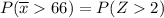
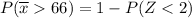
from z tables