Question

Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.

Freshmen 83
Sophomores 68
Juniors 85
Seniors 64
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.

Answer 1

There has been no change in the classifications between the last school year and this school year.

Explanation:

A Chi-square test for goodness of fit will be used in this case.

The hypothesis can be defined as:

H₀: The observed frequencies are same as the expected frequencies.

Hₐ: The observed frequencies are not same as the expected frequencies.

The test statistic is given as follows:

`\chi^(2)=\sum\limits^(n)_(i=1)((O_(i)-E_(i))^(2))/(E_(i))`

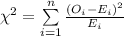
The expected values are computed using the formula:

`E_(i)=p_(i)* N`

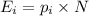
Here, N = 300

Use Excel to compute the values.

The test statistic value is:

`\chi^(2)=\sum\limits^(n)_(i=1)((O_(i)-E_(i))^(2))/(E_(i))=1.662`

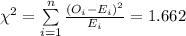
The test statistic value is, 1.662.

The degrees of freedom of the test is:

n - 1 = 4 - 1 = 3

The significance level is, α = 0.05.

Compute the p-value of the test as follows:

p-value = 0.6454

*Use a Chi-square table.

p-value = 0.6454 > α = 0.05.

So, the null hypothesis will not be rejected at 5% significance level.

Thus, concluding that there has been no change in the classifications between the last school year and this school year.