Question

In the diagram, points Q, R, S and T are collinear and PR = RS. IF RS = 12 and RT = 30, find

a) QR
b) ST
c) QS
d) QT​

Answer 1

QR=12

ST=18

QS=24

QT=42

Explanation:

The question tells us that PR is congruent to RS. But there's no point P in the line. So, I'm going to assume it's a typo and that they meant point Q.

So, we know that QR is congruent so RS. RS is 12 and RT is 30. With that information, we can find the other lengths:

1) QR

Since QR is congruent to RS and RS is 12, this means that QR is also 12.

2) ST

We know that RT is 30. RT is made by adding up RS and ST. In an equation, this is:

`RT=RS+ST`

We know that RT is 30 and RS is 12. Thus, substitute:

`30=12+ST\\ST=18`

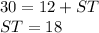
Thus, ST is 18.

3) QS

QS is the length of QR plus RS. Since QR is 12 and RS is also 12, QS is 12+12 or 24.

4) QT is the length of the entire segment. The entire segment can be written as:

`QT=QR+RT`

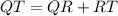
And since we already know that QR is 12 and RT is 30:

`QT=12+30\\QT=42`

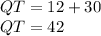
QT is 42.