Answer:
The distance between the grocery store and the school is 4 miles.
Explanation:
Given that each point is represented in rectangular form. The staight-line distance (
 ) between two points on a plane is given by the Pythagorean Theorem:
) between two points on a plane is given by the Pythagorean Theorem:
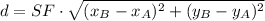
Where:
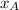 ,
,
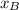 - Horizontal locations of points A and B, dimensionless.
- Horizontal locations of points A and B, dimensionless.
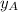 ,
,
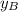 - Vertical locations of points A and B, dimensionless.
- Vertical locations of points A and B, dimensionless.
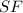 - Scale factor, measured in miles.
- Scale factor, measured in miles.
If
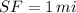 ,
,
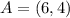 and
and
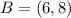 , the straight line distance is:
, the straight line distance is:

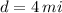
The distance between the grocery store and the school is 4 miles.