Answer:
a.

b.

Explanation:
a. Given,
Perimeter of rectangular field ( P ) = 310 m
Length of the field ( L ) = 84 m
Width of the field ( W ) = ?
Finding the width of the rectangular field

plug the values
⇒
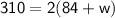
Distribute 2 through the parentheses
⇒
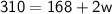
Swap the sides of the equation
⇒

Move 168 to right hand side and change it's sign
⇒
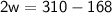
Subtract 168 from 310
⇒
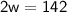
Divide both sides of the equation by 2
⇒
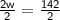
Calculate
⇒
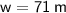
Width = 71 meters
------------------------------------------------------------
2. Given,
Area of rectangular painting ( A ) = 5185 cm²
Width of the painting ( w ) = 61 cm
Length of the painting ( l ) = ?
Finding length of the painting

plug the values
⇒
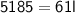
Swap the sides of the equation
⇒

Divide both sides of the equation by 61
⇒
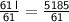
Calculate
⇒
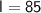 cm
cm
Length = 85 cm
Hope I helped!
Best regards !!!