Question

If a base is negative, how will you know whether the answer is positive or negative before evaluating it?​

Answer 1

Sample Response: When evaluating a power with a negative base, the solution is positive or negative depending on whether the exponent is odd or even. If odd, the value will be negative. If even, the value will be positive.

Explanation:

Answer 2

Explained below.

Explanation:

Assuming that the question is related to exponents.

Consider the expression:
`a^(b)`

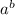
Here,

a = base

b = exponent

Consider that the value of base is a negative term.

Then an even exponent will give a positive result.

And an odd exponent will give a negative result.

Consider the following values of b and suppose that a = -x.

For b = 4,

`a^(b)=(-x)^(4)=(-x)* (-x)* (-x)* (-x)=x`

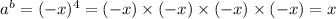
For b = 3,

`a^(b)=(-x)^(3)=(-x)* (-x)* (-x) = -x`