Question

Can someone help explain how i would solve this using the pascals triangle? Like how to convert it into (x + 4)^3 = ax^b+cx^d+ex^f+g

Answer 1

Pascal's triangle is a way of organizing the coefficients in the binomial expansion,
`(a+b)^n`:

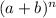n = 0 => 1

n = 1 => 1 1

n = 2 => 1 2 1

n = 3 => 1 3 3 1

n = 4 => 1 4 6 4 1

and so on, where each row starts and ends with a 1, and the numbers in the middle are obtained by adding together the two numbers directly above and to the left. These coefficients are then mulitplied by descending powers of a and descending powers of b (or vice versa, because the pattern is symmetric), starting with 0 and going up to n.

In this case, we have

`(x+4)^3=1\cdot x^3\cdot4^0+3\cdot x^2\cdot4^1+3\cdot x^1\cdot4^2+1\cdot x^0\cdot4^3`

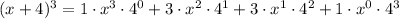
Notice how the powers of x and 4 always sum to n = 3.

Simplifying, we get

`(x+4)^3=x^3+12x^2+48x+64`

so that

a = 1

b = 3

c = 12

d = 2

e = 48

f = 1

g = 64