Question

Which constants could each equation be multiplied by to eliminate the x-variable using addition in this system of equations? 2 x + 3 y = 25. Negative 3 x + 4 y = 22. The first equation can be multiplied by –3 and the second equation by 2. The first equation can be multiplied by –4 and the second equation by 2. The first equation can be multiplied by 3 and the second equation by 2. The first equation can be multiplied by 4 and the second equation by –3.

Answer 1

C is correct

Explanation:

Answer 2

The first equation can be multiplied by 3 and the second equation by 2.

Explanation:

We are given the following system of equations:

`\boxed{\left \{ {{2x+3y=25} \atop {-3x+4y=22}} \right.}`

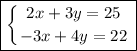
To eliminate a variable in the equation, they must cancel out. For instance, if x = 1, in order to cancel out the numbers, you must add -1.

To multiply an equation, you must apply the constant that you are multiplying by to all constants and coefficients of the equation. For example, to multiply 2x + 4y = 8 by 3, you must multiply 2x by 3, 4y by 3, and 8 by 3.

Therefore, using this information, you can attempt each answer set and test the possibilities.

Answer Choice A

If you multiply the first equation by -3, you will get -6x - 9y = -75. If you multiply the second equation by 2, you will get -6x + 8y = 44. Adding -6 + -6 gives you -12, so these do not cancel out.

Answer Choice B

If you multiply the first equation by -4, you will get -8x - 12y = -100. If you multiply the second equation by 2, you will get -6x + 8y = 44. Adding -8 + -6 gives you -14, so these do not cancel out.

Answer Choice C

If you multiply the first equation by 3, you will get 6x + 9y = 75. If you multiply the second equation by 2, you will get -6x + 8y = 44. Adding 6 + -6 gives you 0, so these do cancel out.

Answer Choice D

If you multiply the first equation by 4, you will get 8x + 12y = 100. If you multiply the second equation by -3, you will get 9x - 12y = -66. Adding 8 + -9 gives you -1, so these do not cancel out.