Answer:
(a) Yes, the data suggest that females are more likely to graduate from high school than males.
(b) A 95% confidence interval for the difference in the graduation rates between females and males is [0.024, 0.404] .
Explanation:
We are given that a survey of over 25,000 Americans aged between 18 and 24 years revealed the following: 88.1% of the 12,678 females and 84.9% of the 12,460 males had high school diplomas.
Let
 = population proportion of females who had high school diplomas.
= population proportion of females who had high school diplomas.
 = population proportion of males who had high school diplomas.
= population proportion of males who had high school diplomas.
(a) So, Null Hypothesis,
 :
:
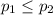 {means that females are less or equally likely to graduate from high school than males}
{means that females are less or equally likely to graduate from high school than males}
Alternate Hypothesis,
 :
:
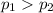 {means that females are more likely to graduate from high school than males}
{means that females are more likely to graduate from high school than males}
The test statistics that will be used here is Two-sample z-test statistics for proportions;
T.S. = ~ N(0,1)
where,
 = sample proportion of females having high school diplomas = 88.1%
= sample proportion of females having high school diplomas = 88.1%
 = sample proportion of males having high school diplomas = 84.9%
= sample proportion of males having high school diplomas = 84.9%
 = sample of females = 12,678
= sample of females = 12,678
= sample of males = 12,460
So, the test statistics =
= 7.428
The value of the standardized z-test statistic is 7.428.
Now, at a 5% level of significance, the z table gives a critical value of 1.645 for the right-tailed test.
Since the value of our test statistics is more than the critical value of z as 7.428 > 1.645, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.
Therefore, we conclude that females are more likely to graduate from high school than males.
(b) Firstly, the pivotal quantity for finding the confidence interval for the difference in population proportion is given by;
P.Q. =
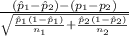 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of females having high school diplomas = 88.1%
= sample proportion of females having high school diplomas = 88.1%
 = sample proportion of males having high school diplomas = 84.9%
= sample proportion of males having high school diplomas = 84.9%
 = sample of females = 12,678
= sample of females = 12,678
 = sample of males = 12,460
= sample of males = 12,460
Here for constructing a 95% confidence interval we have used a Two-sample z-test statistics for proportions.
So, 95% confidence interval for the difference in population proportions, (
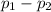 ) is;
) is;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level
of significance are -1.96 & 1.96}
P(-1.96 <
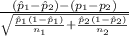 < 1.96) = 0.95
< 1.96) = 0.95
P(
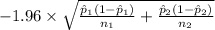 <
<
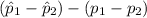 <
<
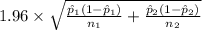 ) = 0.95
) = 0.95
P(
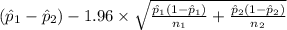 < (
< (
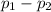 ) <
) <
 ) = 0.95
) = 0.95
95% confidence interval for (
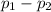 ) = [
) = [
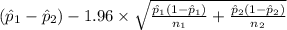 ,
,
 ]
]
= [
 ,
,
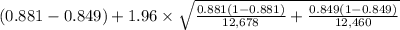 ]
]
= [0.024, 0.404]
Therefore, a 95% confidence interval for the difference in the graduation rates between females and males is [0.024, 0.404] .
(c) The assumptions and conditions necessary for the above inferences to hold are;
- The data must follow the normal distribution.
- The sample must be taken from the population data only or the sample represents the population data.