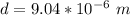Answer:
The distance of separation is
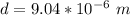
Step-by-step explanation:
From the question we are told that
The wavelength is
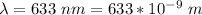
The distance of the screen is
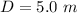
The distance between the fringes is
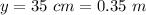
Generally the distance between the fringes is mathematically represented as
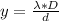
Here d is the distance of separation between the slit
=>
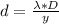
=>
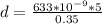
=>