Answer:
a
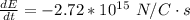
b
The direction of the electric field is opposite that of the current
Step-by-step explanation:
From the question we are told that
The current is
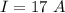
The diameter of the ring is
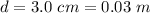
Generally the radius is mathematically represented as
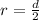
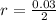

The cross-sectional area is mathematically represented as
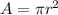
=>
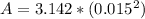
=>

Generally according to ampere -Maxwell equation we have that
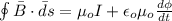
Now given that
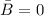 it implies that
it implies that
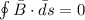
So
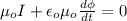
Where
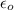 is the permittivity of free space with value
is the permittivity of free space with value
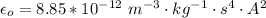
 is the permeability of free space with value
is the permeability of free space with value
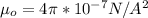
 is magnetic flux which is mathematically represented as
is magnetic flux which is mathematically represented as
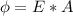
Where E is the electric field strength
So
![\mu_o I + \epsilon_o \mu _o ( d [EA] )/(dt ) = 0](https://img.qammunity.org/2021/formulas/physics/college/tyxmai9tnemoeuhusmku81xx3ddy9grxve.png)
=>
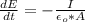
=>
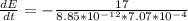
=>
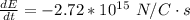
The negative sign shows that the direction of the electric field is opposite that of the current