Answer:
λ = hc/(eV + h
)
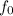Step-by-step explanation:
Let the work function of the metal = ∅
the kinetic energy with which the electrons are ejected = E
the energy of the incident electromagnetic wave = hf
Then, we know that the kinetic energy of the emitted electron will be
E = hf - ∅
because the energy of the incident electromagnetic radiation must exceed the work function for electrons to be ejected.
This means that the energy of the incident e-m wave can be written as
hf = E + ∅
also, we know that the kinetic energy of the emitted electron E = eV
and the work function ∅ = h
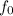
we can they combine all equations to give
hf = eV + h
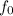
we know that f = c/λ
substituting, we have
hc/λ = eV + h
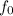
λ = hc/(eV + h
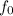) This is the wavelength of the e-m radiation needed to eject electrons from a metal.
where
λ is the wavelength of the e-m radiation
h is the Planck's constant = 6.63 x 10^-34 m^2 kg/s
c is the speed of e-m radiations in a vacuum = 3 x 10^8 m/s
e is the charge on an electron
V is the voltage potential on the electron
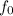is the threshold frequency of the metal