Question

A manufacturer claims that the calling range (in feet) of its 900-MHz cordless telephone is greater than that of its leading competitor. A sample of 9 phones from the manufacturer had a mean range of 1260 feet with a standard deviation of 24 feet. A sample of 12 similar phones from its competitor had a mean range of 1230 feet with a standard deviation of 37 feet. Do the results support the manufacturer's claim? Let μ1 be the true mean range of the manufacturer's cordless telephone and μ2 be the true mean range of the competitor's cordless telephone. Use a significance level of α=0.1 for the test. Assume that the population variances are equal and that the two populations are normally distributed.

a. State the null and alternative hypotheses for the test.
b. Compute the value of the t test statistic. Round your answer to three decimal places.
c. Determine the decision rule for rejecting the null hypothesis H0. Round your answer to three decimal places.
d. State the test's conclusion.

Answer 1

a

The null hypothesis is
`H_o : \mu_1 - \mu_2 \le 0`

The alternative hypothesis is
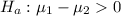`H_a : \mu_1 - \mu_2 > 0` (Manufacturers claim)

b

`t = 2.114`

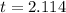
c

Decision rule

Reject the null hypothesis

d

There is sufficient evidence to support the claim that the calling range (in feet) of Manufacturers 900-MHz cordless telephone is greater than that of its leading competitor

Explanation:

From the question we are told that

The first sample size is
`n_1 = 9`

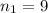
The second sample size is
`n_2 = 12`

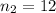
The first sample mean is
`\= x_1 = 1260 \ feet`

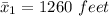
The second sample mean is
`\= x_2 = 1230`

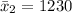
The first standard deviation is
`\sigma_1 = 24`

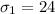
The second standard deviation is
`\sigma_2 = 37`

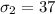
The significance level is
`\alpha = 0.10`

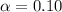
The null hypothesis is
`H_o : \mu_1 - \mu_2 \le 0`

The alternative hypothesis is
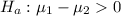`H_a : \mu_1 - \mu_2 > 0` (Manufacturers claim)

Generally the degree of freedom is mathematically represented as

`df = n_1 + n_2 -2`

`df = 9 + 12 - 2`

`df = 19`

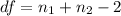
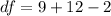
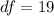
Generally the pooled standard deviation is mathematically represented as

`\sigma_p = \sqrt{ ((n_1 - 1)\sigma_1^2 + (n_2-1 )\sigma_2^2 )/( (n_1 - 1 ) + (n_2 - 1 )) }`

`\sigma_p = \sqrt{ ((9 - 1)24^2 + (12-1 )37^2 )/( (9 - 1 ) + (12 - 1 )) }`

`\sigma_p =32.17`

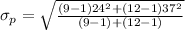
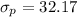
Generally the test statistics is mathematically represented as

`t = \frac{\= x_1 - \= x_2 }{\sqrt{(\sigma_p^2)/(n_1 ) +(\sigma_p^2)/(n_2 ) } }`

`t = \frac{1260 - 1230 }{\sqrt{(32.17^2)/(9 ) +(32.17^2)/(12 ) } }`

`t = 2.114`

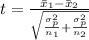
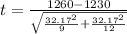
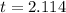
Generally the p-value is obtained from the student t distribution table and the value is

`p-value = P(t > 2.11) = t_(2.11 , 19) = 0.024173`

Given that the
`p-value < \alpha`

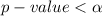
The null hypothesis is rejected

Hence we can conclude that there is sufficient evidence to support the claim that the calling range (in feet) of Manufacturers 900-MHz cordless telephone is greater than that of its leading competitor