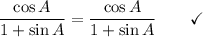Answer: see both proofs below
Explanation:
Use Difference Identity: tan (A - B) = (tan A - tan B)/(1 + tanA · tanB)
Use Unit Circle to evaluate: tan (π/4) = 1
Use Tangent Identity: tanA = (sinA)/(cosA)
Use Half-Angle Identities:
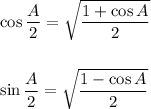
Part 1 Proof LHS → Middle
LHS:
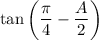
Difference Identity:
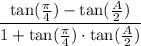
Unit Circle:
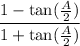
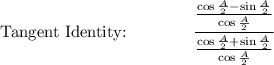
Simplify:
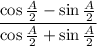
LHS = Middle:
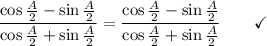
Part 2 Proof Middle → RHS
Middle:
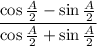
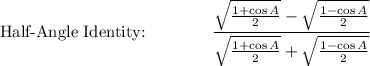
Simplify:
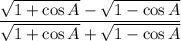
Rationalize Denominator:
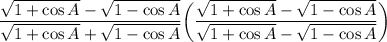
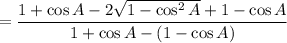
Simplify:
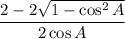
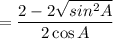
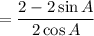
Factor:
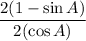
Simplify:
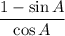
Expand:
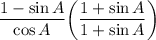
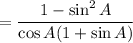
Simplify:
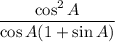
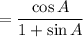
Middle = RHS: