Answer:
see explanation
Explanation:
Using the double angle identity for cosine
cos2x = 2cos²x - 1
Given
cos(
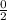 ) =
) =
 ( p +
( p +
 ) , then
) , then
cosΘ = 2[
 (p +
(p +
 ) ]² - 1
) ]² - 1
= 2 [
 (p² + 2 +
(p² + 2 +
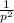 ) ] - 1 ← distribute by 2
) ] - 1 ← distribute by 2
=
 (p² + 2 +
(p² + 2 +
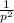 ) - 1 ← distribute by
) - 1 ← distribute by

=
 p² + 1 +
p² + 1 +
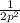 - 1
- 1
=
 p² +
p² +
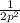 ← factor out
← factor out
 from each term
from each term
=
 ( p² +
( p² +
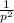 ) ← as required
) ← as required