Question

(Please help! :( savvas Realize sucks I don't understand)

_______________________________

Find the coordinates of the point 7/10 of the way from A to B. (see picture for graph).

The coordinates of the point 7/10 of the way from A to B are ________.
(Type an ordered pair.)​

Answer 1

The coordinates of the point
`\( (7)/(10) \)` of the way from A to B are
`\( (5.4, 2.7) \)` .

To find the coordinates of the point
`\( (7)/(10) \)` of the way from point A to point B, we can use the formula for finding a point on a line segment.

The coordinates of point A are
`\((-3, -5)\)`, and the coordinates of point B are
`\((9, 6)\)`. The formula for finding a point
`\( P \)` that is
`\( t \)` of the way from point
`( A \))` to point
`\( B \)` is given by:

`\[ P = (1 - t) \cdot A + t \cdot B \]`

In this case,
`\( t = (7)/(10) \)`. Substituting the values:

`\[ P = (1 - (7)/(10)) \cdot (-3, -5) + (7)/(10) \cdot (9, 6) \]`

`\[ P = ((3)/(10) \cdot (-3, -5)) + ((7)/(10) \cdot (9, 6)) \]`

`\[ P = (-0.9, -1.5) + (6.3, 4.2) \]`

Adding the corresponding coordinates:

`\[ P = (5.4, 2.7) \]`

Therefore, the coordinates of the point
`\( (7)/(10) \)` of the way from A to B are
`\( (5.4, 2.7) \)`.

Answer 2

(5.4, 2.7)

Explanation:

The coordinates of the point 7/10 of the way from A to B is given by the relation;

(x₁ + m×(x₂ - x₁), y₁ + m×(y₂ - y₁))

Where the coordinate of point A is (-3, -5) and the coordinates of the point B is (9, 6) we have;

x₁ = -3

m = 7/10

x₂ = 9

y₁ = -5

y₂ = 6

Substituting the values into the above equation gives;

-3 + 7/10 × (9 - (-3)), -5 + 7/10 × (6 - (-5)) = (5.4, 2.7)

The coordinate of the point P, 7/10 from A is (5.4, 2.7)

We check the length of the point from A to B to give;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}` =

`l_(AB) = \sqrt{\left (6-(-5) \right )^(2)+\left (9-(-5) \right )^(2)} = √(265)`

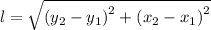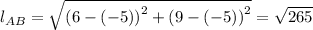
the length of the point from A to B gives

`l_(AB) = \sqrt{\left (2.7-(-5) \right )^(2)+\left (5.4-(-5) \right )^(2)} = (7)/(10) * √(265)`

The coordinate of the point 7/10 of the way from A to B are (5.4, 2.7).