Question

I need help, I'm completely lost

Answer 1

alpha = 2

beta = -6

Explanation:

let everything inside the ln be 'a'

use the chain rule to to differentiate ln a with respect to a

since the differentiation of lnx is 1/x , the differentiation of lna will be 1/a

after the differentiation, you will get:
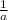`(1)/(a)` X
`(d[(x+1)^(2)X (2x-1)^(2) ] )/(dx)`

you need to use the product rule to differentiate the second part, then multiply 1/a by both the equations being added

replace a with its actual value

you will get
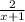`(2)/(x + 1)` and
`(-6)/(2x -1)`

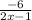
by comparing it to the given equation, we get α = 2 and β = -6