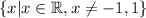Question

Find the domain of
`(4)/(x^2-1)`

Answer 1

`\large \boxed{\mathrm{All \ real \ numbers \ except} \ x=-1 \ \mathrm{and} \ x=1}`

Explanation:

`\displaystyle (4)/(x^2-1)`

The domain of a rational function is all the real numbers except the numbers for which the denominator is equal to 0.

Let the denominator equal to 0.

`x^2-1=0`

Solve for x.

`x^2 =1 \\ \\ \\ x= -1 \ \mathrm{or} \ x=1`

When x = -1 and x = 1, the function is undefined.

The domain of the function is all real numbers except x = -1 and x = 1.

Answer 2

See below.

Explanation:

We have the rational function:

`(4)/(x^2-1)`

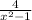
The domains of rational function are the zeros of the denominator. This is because if the denominator equals 0, they the function would be undefined.

Therefore, we need to find the zeros of the denominator. Set the expression in the denominator to zero:

`x^2-1=0`

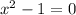
Solve for x. Add 1 to both sides:

`x^2=1`

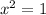
Take the square root of both sides:

`x=\pm \sqrt1`

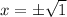
Simplify:

`x=\pm 1`

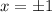
So, the domain is all real numbers except for x=-1 and x=1.

In interval notation, this is:

`(-\infty,-1)\cup(-1,1)\cup(1,\infty)`

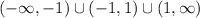
This is interpreted as all values until -1 not including -1 until all values until 1 not including 1, and then all values there on after.

In set notation, this is:

`\{x|x\in\mathbb{R}, x\\eq-1, 1\}`