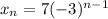Question

Find an equation for the nth term of a geometric sequence where the second and fifth terms are -21 and 567, respectively

Answer 1

`x_n=7(-3)^(n-1)`

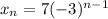
Explanation:

First, write some equations so we can figure out the common ratio and the initial term. The standard explicit formula for a geometric sequence is:

`x_n=ar^(n-1)`

Where xₙ is the nth term, a is the initial value, and r is the common ratio.

We know that the second and fifth terms are -21 and 567, respectively. Thus:

`a_2=-21\\a_5=567`

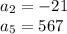
Substitute them into the equations:

`x_2=ar^((2)-1)\\-21=ar`

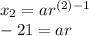
And:

`a^5=ar^((5)-1)\\567=ar^4`

To find a and r, divide both sides by a in the first equation:

`r=-(21)/(a)`

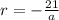
And substitute this into the second equation:

`567=a((-21)/(a) )^4`

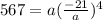
Simplify:

`567=a(((-21)^4)/(a^4))`

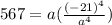
The as cancel out. (-21)^4 is 194481:

`(567)/(1)=(194481)/(a^3)`

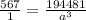
Cross multiply:

`194481=567a^3\\a^3=194481/567=343`

Take the cube root of both sides:

`a=\sqrt[3]{343} =7`

Therefore, the initial value is 7.

And the common ratio is (going back to the equation previously):

`r=-21/a\\r=-21/(7)\\r=-3`

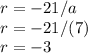
Thus, the common ratio is -3.

Therefore, the equation is:

`x_n=7(-3)^(n-1)`