Answer:
Equilibrium constant expression for
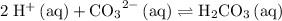 :
:
![\displaystyle K = \frac{\left(a_{\mathrm{H_2CO_3\, (aq)}}\right)}{\left(a_{\mathrm{H^(+)}}\right)^2\, \left(a_{\mathrm{{CO_3}^(2-)\, (aq)}}\right)} \approx \frac{[\mathrm{H_2CO_3}]}{\left[\mathrm{H^(+)\, (aq)}\right]^(2) \, \left[\mathrm{CO_3}^(2-)\right]}](https://img.qammunity.org/2021/formulas/chemistry/college/pokxyttpxpmdmdo52rty7mnlxmcj0j2fy2.png) .
.
Where
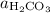 ,
,
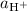 , and
, and
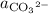 denote the activities of the three species, and
denote the activities of the three species, and
![[\mathrm{H_2CO_3}]](https://img.qammunity.org/2021/formulas/chemistry/college/hsh6b8e6awafibyqqc97w7u875ffalmbi1.png) ,
,
![\left[\mathrm{H^(+)}\right]](https://img.qammunity.org/2021/formulas/chemistry/college/v0wljc03rmwzs4mxsl5wmzsuutnvm8zoea.png) , and
, and
![\left[\mathrm{CO_3}^(2-)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/p67rwkajecq9zha1l9b8xkvrxb6y2c3luz.png) denote the concentrations of the three species.
denote the concentrations of the three species.
Step-by-step explanation:
Equilibrium Constant Expression
The equilibrium constant expression of a (reversible) reaction takes the form a fraction.
Multiply the activity of each product of this reaction to get the numerator.
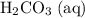 is the only product of this reaction. Besides, its coefficient in the balanced reaction is one. Therefore, the numerator would simply be
is the only product of this reaction. Besides, its coefficient in the balanced reaction is one. Therefore, the numerator would simply be
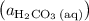 .
.
Similarly, multiply the activity of each reactant of this reaction to obtain the denominator. Note the coefficient "
 " on the product side of this reaction.
" on the product side of this reaction.
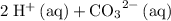 is equivalent to
is equivalent to
 . The species
. The species
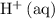 appeared twice among the reactants. Therefore, its activity should also appear twice in the denominator:
appeared twice among the reactants. Therefore, its activity should also appear twice in the denominator:
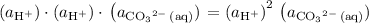 .
.
That's where the exponent "
 " in this equilibrium constant expression came from.
" in this equilibrium constant expression came from.
Combine these two parts to obtain the equilibrium constant expression:
![\displaystyle K = \frac{\left(a_{\mathrm{H_2CO_3\, (aq)}}\right)}{\left(a_{\mathrm{H^(+)}}\right)^2\, \left(a_{\mathrm{{CO_3}^(2-)\, (aq)}}\right)} \quad\begin{matrix}\leftarrow \text{from products} \\[0.5em] \leftarrow \text{from reactants}\end{matrix}](https://img.qammunity.org/2021/formulas/chemistry/college/911tt4yfpx9o5crd8kw39xqe3e55fbsl6g.png) .
.
Equilibrium Constant of Concentration
In dilute solutions, the equilibrium constant expression can be approximated with the concentrations of the aqueous "
 " species. Note that all the three species here are indeed aqueous. Hence, this equilibrium constant expression can be approximated as:
" species. Note that all the three species here are indeed aqueous. Hence, this equilibrium constant expression can be approximated as:
![\displaystyle K = \frac{\left(a_{\mathrm{H_2CO_3\, (aq)}}\right)}{\left(a_{\mathrm{H^(+)}}\right)^2\, \left(a_{\mathrm{{CO_3}^(2-)\, (aq)}}\right)} \approx \frac{\left[\mathrm{H_2CO_3\, (aq)}\right]}{\left[\mathrm{H^(+)\, (aq)}\right]^2\cdot \left[\mathrm{{CO_3}^(2-)\, (aq)}\right]}](https://img.qammunity.org/2021/formulas/chemistry/college/k9lfwugknyfl3mu1lki2zwoi1qygv413ot.png) .
.