Question

How many three-digit natural numbers can be formed using only the even digits, if the numbers can contain each of these digits only once?

Answer 1

48

Explanation:

Solution 1:

There are 5 even digits: 0, 2, 4, 6, and 8, and
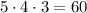`5\cdot 4\cdot 3=60` ways to arrange any three of them in order: 5 ways to pick the first digit, 4 ways to pick the second digit, and 3 ways to pick the third.

Another way to think about this is there are
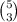`5\choose 3` ways to pick any three of the digits, and
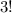`3!` ways to rearrange them, so there are
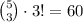`{5\choose 3 }\cdot 3!=60` ways to pick and arrange 3 of the digits.

Then, we have to subtract cases where 0 is the first digit, because that would give us numbers such as 028 or 042 which are not three-digit natural numbers.

When 0 is the first digit, there are 4 possibilities for the second digit and 3 possibilities for the third digit, so there are
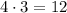`4\cdot3=12` ways for 0 to be the first digit.

These are the cases we don't want, so we subtract them from the total cases we can arrange any three of the digits. This gives us

`60-12=\boxed{48}`

total ways.

Solution 2:

We split the possible arrangements into two different cases: when we use the digits without 0 and when we do use the digit 0.

Case 1: we use 0:

We first pick the three numbers we use: one of them has to be 0, so there are
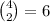`{4\choose 2}=6` ways to pick the other two numbers.

Then, since 0 cannot be the first digit, there are 2 ways to pick the first digit. We used a digit for the first number, so there are 2 more numbers we can choose from, including 0, for the second digit. There is only one possibility for the last digit, so we have
`2\cdot2\cdot1=4` ways to pick the order.

So, multiplying this by the number of ways there are to pick the numbers, there are
`6\cdot4=24` ways for this case.

Case 2: we don't use 0:

If we don't use 0, there are 4 digits we can choose from: 2, 4, 6, and 8. There are 4 ways to choose the first digit, 3 ways to chose the second digit, and 2 ways for the third.

So, we have
`4\cdot3\cdot2=24` ways for this case.

Combining the cases, there are
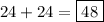`24+24=\boxed{48}` total possible ways to form a three-digit natural number using only the even digits.