Question

Solve and graph the compound inequalities. (You don’t need to graph it on a line plot but if you could that would be great!)

A) -12 < 5x - 2 < 13



B) 3x < -9 or 2x ≥ x + 1

Answer 1

Part A

`-12 < 5x - 2 < 13\\\\-12+2 < 5x - 2+2 < 13+2 \ \text{ ... add 2 to all sides}\\\\-10 < 5x < 15\\\\-10/5 < 5x/5 < 15/5 \ \text{ ... divide all sides by 5 to isolate x}\\\\-2 < x < 3\\\\`

To graph this, we plot open holes at -2 and 3 on the number line. Shade between these open holes to represent values between -2 and 3, but we don't include the endpoints.

See figure 1 below.

===============================================

Part B

Solve the first inequality to get

`3x < -9\\\\3x/3 < -9/3\\\\x < -3\\\\`

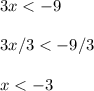
Now solve the second inequality

`2x \ge x+1\\\\2x-x \ge x+1-x\\\\x \ge 1\\\\`

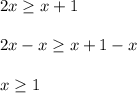
We have
`x < -3 \ \text{ or } \ x \ge 1`

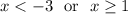
The graph will have an open hole at -3 and a closed/filled in circle at 1. We shade everywhere but the region between these marked values. The left portion in blue represents stuff smaller than -3; the right portion in red represents values equal to 1 or larger.

See figure 2 below.