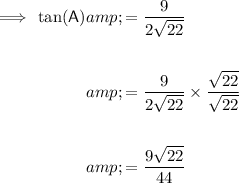Question

Need help with trigonometry

Answer 1

`\boxed{ \sf \bold{tanA = (9)/(2√(22) ) }}`

Given:

• c = 13

• b = 2√22

=============

Formula's:

• tan(x) = opposite/adjacent : tane rule

• a² + b² = c² : Pythagoras Theorem

=============

To find Tan A, first find opposite side of angle A and adjacent side which is already given of 2√22

=============

Opposite side:

• (2√22)² + b² = 13²

• b² = 169 - 88

• b² = 81

• b = √81

• b = 9

Now find tan A:

tanA = 9/2√22

Answer 2

`\sf \tan(A) & =(9√(22))/(44)`

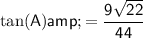
Explanation:

If angle C is the right angle, then side c is the hypotenuse.

Use Pythagoras' Theorem
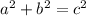`a^2+b^2=c^2` to find the length of side a:

Given:

• b = 2√22
• c = 13

`\implies a^2+(2 √(22))^2=13^2`

`\implies a^2+88=169`

`\implies a^2=81`

`\implies a=√(81)`

`\implies a=9`

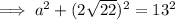
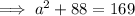
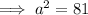
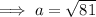
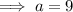
Tan Trig Ratio

`\sf \tan(\theta)=(O)/(A)`

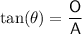
where:

• 
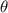  `\theta` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle

Given:

• 
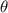  `\theta` = A
• O = side opposite angle A = a = 9
• A = side adjacent angle A = b = 2√22

`\begin{aligned}\implies \sf \tan(A) & =(9)/(2√(22))\\\\ & =(9)/(2√(22)) * (√(22))/(√(22))\\\\ & = (9√(22))/(44) \end{aligned}`