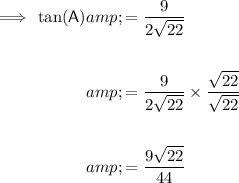Answer:
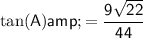
Explanation:
If angle C is the right angle, then side c is the hypotenuse.
Use Pythagoras' Theorem
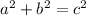 to find the length of side a:
to find the length of side a:
Given:
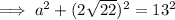
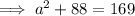
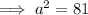
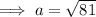
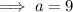
Tan Trig Ratio

where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
Given:
 = A
= A- O = side opposite angle A = a = 9
- A = side adjacent angle A = b = 2√22