Answer:
See Explanation Section
Explanation:
Given
A base 5 numbering system: Envision
Some of the rules are as follows:
- For a base 5 system, the highest individual digit is 4: Meaning that the 1234, 343, 110 are valid digits while 1235, 78, 55 are invalid digits
- The place values of this system are in place of 5s: i.e. ......5°, 5¹, 5², 5³, 5⁴......
3 digit examples
1
Base 5: 100
Base 10: 25 (See calculation below)
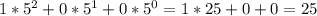
Base 2: 11001 (See calculation below)
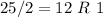
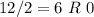
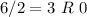
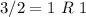
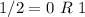
Writing the remainder from bottom: 11001
Using the same steps as used in (1) above
2.
Base 5: 211
Base 10: 56
Base 2: 111000
3.
Base 5: 441
Base 10: 121
Base 2: 1111001
4.
Base 5: 230
Base 10: 65
Base 2: 1000001
5.
Base 5: 342
Base 10: 97
Base 2: 1100001
6.
Base 5: 141
Base 10: 46
Base 2: 101110