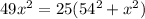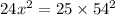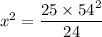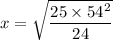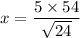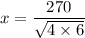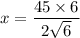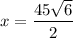Question

You want to get from a point A on the straight shore of the beach to a buoy which is 54 meters out in the water from a point B on the shore. B is 70 meters from you down the shore. If you can swim at a speed of 5 meters per second and run at a speed of 7 meters per second, at what point along the shore, x meters from B, should you stop running and start swimming if you want to reach the buoy in the least time possible

Answer 1

`x =(45 √(6))/( 2)`

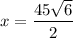
Explanation:

From the given information:

The diagrammatic interpretation of what the question is all about can be seen in the diagram attached below.

Now, let V(x) be the time needed for the runner to reach the buoy;

∴ We can say that,

`\mathtt{V(x) = (70-x)/(7)+(√(54^2+x^2))/(5)}`

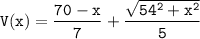
In order to estimate the point along the shore, x meters from B, the runner should stop running and start swimming if he want to reach the buoy in the least time possible, then we need to differentiate the function of V(x) and relate it to zero.

i.e

The differential of V(x) = V'(x) =0

=
`(d)/(dx)\begin {bmatrix} (70-x)/(7) + (√(54^2+x^2))/(5) \end {bmatrix}= 0`

`-(1)/(7)+ (1)/(5)* (x)/(√(54^2+x^2))=0`

`(1)/(5)* (x)/(√(54^2+x^2))= (1)/(7)`

`(5x)/(√(54^2+x^2))= (1)/(7)`

`(x)/(√(54^2+x^2))= (1)/((7)/(5))`

`(x)/(√(54^2+x^2))= (5)/(7)`

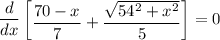
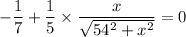
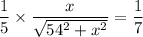
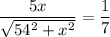
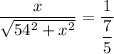
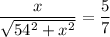
squaring both sides; we get

`(x^2)/(54^2+x^2)= (5^2)/(7^2)`

`(x^2)/(54^2+x^2)= (25)/(49)`

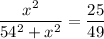
By cross multiplying; we get

`49x^2 = 25(54^2+x^2)`

`49x^2 = 25 * 54^2+ 25x^2`

`49x^2-25x^2 = 25 * 54^2`

`24x^2 = 25 * 54^2`

`x^2 = (25 * 54^2)/(24)`

`x =\sqrt{ (25 * 54^2)/(24)}`

`x =(5 * 54)/(√(24))`

`x =(270)/(√(4 * 6))`

`x =(45 * 6)/( 2 √( 6))`

`x =(45 √(6))/( 2)`