Explanation:
Hey, there!!
Given that,
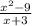
{ we can write (a^2-4) as (a^2 - 2^2) also as (x^2- 9) can be written as (x^2 - 3^2)}.

We have a^2-b^2= (a+b) (a-b), so keep same formula on it.

(x+3) in numerator and denominator gets cancelled,

Therefore, (x-3) is the final value.
Hope it helps...