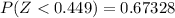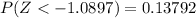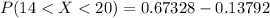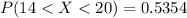Question

Recent census data indicated that 14.2% of adults between the ages of 25 and 34 live with their parents. A random sample of 125 young adults in this age group was selected. What is the probability that between 14 and 20 of these young adults lived with their parents?

Answer 1

The probability is
`P(14 < X < 20 ) = 0.5354`

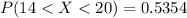
Explanation:

From the question we are told that

The proportion that live with their parents is
`\r p = 0.142`

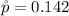
The sample size is n = 125

Given that there are two possible outcomes and that this outcomes are independent of each other then we can say the Recent census data follows a Binomial distribution

i.e

`X \ \~ \ B( \mu , \sigma )`

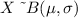
Now the mean is evaluated as

`\mu = n * \r p`

`\mu = 125 * 0.142`

`\mu = 17.75`

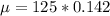
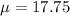
Generally the proportion that are not staying with parents is

`\r q = 1 - \r p`

= >
`\r q = 0.858`

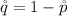
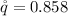
The standard deviation is mathematically evaluated as

`\sigma = √(n * \r p * \r q )`

`\sigma = √( 125 * 0.142 * 0.858 )`

`\sigma = 3.90`

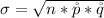
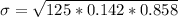
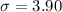
Given the n is large then we can use normal approximation to evaluate the probability as follows

`P(14 < X < 20 ) = P( ( 14 - 17.75)/(3.90) <( X - \mu )/(\sigma ) < ( 20 - 17.75)/(3.90) )`

Now applying continuity correction

`P(14 < X < 20 ) = P( ( 13.5 - 17.75)/(3.90) < ( X - \mu )/(\sigma ) < ( 19.5 - 17.75)/(3.90) )`

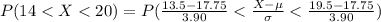
Generally

`( X - \mu )/(\sigma ) = Z ( The \ standardized \ value \ of X )`

`P(14 < X < 20 ) = P( ( 13.5 - 17.75)/(3.90) < Z< ( 19.5 - 17.75)/(3.90) )`

`P(14 < X < 20 ) = P( -1.0897 < Z< 0.449 } )`

`P(14 < X < 20 ) = P( Z< 0.449 ) - P(Z < -1.0897)`

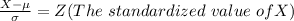
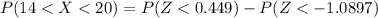
So for the z - table

`P( Z< 0.449 ) = 0.67328`

`P(Z < -1.0897) = 0.13792`

`P(14 < X < 20 ) = 0.67328 - 0.13792`

`P(14 < X < 20 ) = 0.5354`