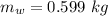Answer:
The mass is
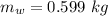
Step-by-step explanation:
From the question we are told that
The mass of ice is
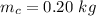
The initial temperature of the ice is
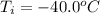
The initial temperature of the water is

The final temperature of the system is
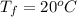
Generally according to the law of energy conservation,
The total heat loss is = total heat gained
Now the total heat gain is mathematically represented as
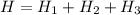
Here
 is the energy required to move the ice from
is the energy required to move the ice from
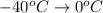
And it mathematically evaluated as

Here the specific heat of ice is
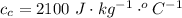
So
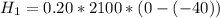
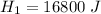
 is the energy to melt the ice
is the energy to melt the ice
And it mathematically evaluated as

The latent heat of fusion of ice is
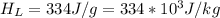
So
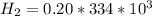
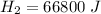
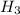 is the energy to raise the melted ice to
is the energy to raise the melted ice to
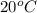
And it mathematically evaluated as

Here the specific heat of water is
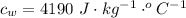
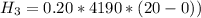
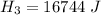
So
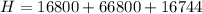
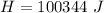
The heat loss is mathematically evaluated as
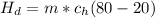

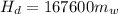
So
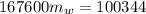
=>