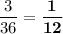Answer:
Explanation:
Given:
Two fair number cubes i.e. two dice consisting the numbers 1, 2, 3, 4, 5, 6 on their faces and have equal probability of each number.
The dice are rolled.
To find:
Probability of getting the sum of two numbers as 4.
Solution:
First of all, let us have a look at the total possibilities when two dice are rolled:
([1][1], [1][2], [1][3], [1][4], [1][5], [1][6],
[2][1], [2][2], [2][3], [2][4], [2][5], [2][6],
[3][1], [3][2], [3][3], [3][4], [3][5], [3][6],
[4][1], [4][2], [4][3], [4][4], [4][5], [4][6],
[5][1], [5][2], [5][3], [5][4], [5][5], [5][6],
[6][1], [6][2], [6][3], [6][4], [6][5], [6][6])
These are total 36 possible outcomes.
For getting a sum as 4:
Possible number of favorable cases are 3 (as highlighted in BOLD in above)
Formula for probability of an event E can be observed as:
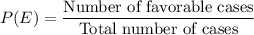
Required probability is: