Answer:
![g(x)=4\sqrt[3]{x}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/z6cghcmjp5sgqzpnzyrg.png)
Explanation:
We can see that the curve has not been translated horizontally or vertically, nor has it been reflected in either axis. Therefore, g(x) is a stretch:


Parent function
![f(x)=\sqrt[3]{x}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/9mwn8cg3jtts5jx54txt.png)
![\implies g(x)=a\:f(x)=a\sqrt[3]{x}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/k3pgjymkxgia1vacip9d.png)
![\textsf{or}\quad g(x)=f(ax)=\sqrt[3]{ax}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8v9f27wt2rw4ow0t3lxn.png)
From inspection of the graph:
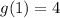
Therefore:
![\implies a\sqrt[3]{1}=4](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ztqv37w548k24hy7xo9k.png)
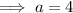
![\implies g(x)=4\sqrt[3]{x}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o5n56f321lg3jvjuh8sw.png)
Or:
![\implies \sqrt[3]{a(1)}=4](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/soerbbapwae5h07mt0zg.png)
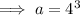
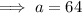
![\implies g(x)=\sqrt[3]{64x}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/onpm7kt6bsxrgwneouxd.png)
![\implies g(x)=\sqrt[3]{64}\sqrt[3]{x}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fhq2znuvpaeihve2x6so.png)
![\implies g(x)=4\sqrt[3]{x}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o5n56f321lg3jvjuh8sw.png)
Therefore, the translated function is:
![g(x)=4\sqrt[3]{x}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/z6cghcmjp5sgqzpnzyrg.png)