Explanation:
Since the sequence above is an arithmetic sequence
For an nth term in an arithmetic sequence
A(n) = a + ( n - 1)d
where a is the first term
n is the number of terms
d is the common difference
From the question
a = 1/3
d = 1/2 - 1/3 = 1/6 or 2/3 - 1/2 = 1/6
Substitute the values into the above formula
That's
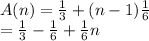
So the nth term of the sequence is
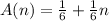
For a50 since we are finding the 50th term
n = 50
So we have

We have the final answer as
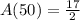
Hope this helps you