Question

Consider an experiment in which a marble is tossed into a box whose base is shown in the figure. The probability that the marble will come to rest in the shaded portion of the box is equal to the ratio of the shaded area to the total area of the figure. If the probability is equal to 3/10, find the positive value of x.

Answer 1

x = 2

Explanation:

Probability that the marble comes to rest in the shaded region is equal to the ratio of the shaded area to the total area.

Probability 'P' =
`(A')/(A)`

Area of the shaded region (A')= (x + 1)(x + 2)

Total area of the figure (A) = (2x + 1)(3x + 2)

P =
`((x+1)(x+2))/((2x+1)(3x+2))=(3)/(10)`

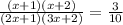
10(x + 1)(x + 2) = 3(2x + 1)(3x + 2)

10(x² + 3x + 2) = 3(6x² + 7x + 2)

10x² + 30x + 20 = 18x² + 21x + 6

(18x² - 10x²) + (21x - 30x) + (6 - 20) = 0

8x² - 9x - 14 = 0

x =
`(9\pm√((-9)^2-4(8)(-14)) )/(2(8))`

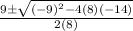
x =
`(9\pm √(81+448))/(16)`

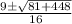
x =
`(9\pm 23)/(16)`

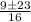
x = -
`(7)/(8), 2`

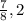
Therefore, positive value of x = 2 will be the answer.