Question

the amount of gas in sarahs car is uniformly distributed between 1 and 16 gallons. Calculate the probability that the amount of gas is exactly 7 gallons

Answer 1

The probability that the amount of gas in Sarah's car is exactly 7 gallons is 0.067.

Explanation:

Let the random variable X represent the amount of gas in Sarah's car.

It is provided that
`X\sim Unif(1, 16)`.

The amount of gas in a car is a continuous variable.

So, the random variable X follows a continuous uniform distribution.

Then the probability density function of X is:

`f_(X)(x)=(1)/(b-a);\ a<X<b`

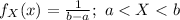
For a continuous probability distribution the probability at an exact point is 0.

So, to compute the probability that the amount of gas in Sarah's car is exactly 7 gallons use continuity correction on both sides:

P (X = 7) = P (7 - 0.5 < X < 7 + 0.5)

= P (6.5 < X < 7.5)

`=\int\limits^(7.5)_(6.5) {(1)/(16-1)} \, dx \\\\=(1)/(15)* |x|^(7.5)_(6.5)\\\\=(1)/(15)* (7.5-6.5)\\\\=(1)/(15)\\\\=0.0666667\\\\\approx 0.067`

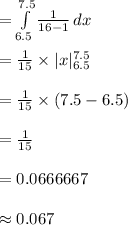
Thus, the probability that the amount of gas in Sarah's car is exactly 7 gallons is 0.067.